Systèmes de deux équations à deux inconnues.

Définition: Soient a, b et c trois nombres réels donnés. Une équation du type , ou s'y ramenant, est une équation à deux inconnues du premier degré

Exemple: est une équation à deux inconnues du premier degré.

Définition: On appelle solution d'une équation à deux inconnues du premier degré du type tout couple (x;y) tel que l'égalité soit vraie.

Exemple: n'est pas un couple solution de, car .

Par contre, le couple est solution de , car .

Définition: On appelle système de deux équations à deux inconnues du premier degré la donnée simultanée de deux équations à deux inconnues du premier degré.

Exemple : est un système de deux équations à deux inconnues du premier degré.

Définition: Résoudre un tel système, c’est trouver tous les couples, si ils existent pour lesquels les deux égalités soient vraies simultanément.

Nota Bene: En classe de troisième, on supposera systématiquement que les systèmes résolus sont des « bons systèmes » admettant toujours une unique solution.

Méthode de résolution :

Le principe général est d’éliminer une inconnue pour se ramener à la résolution d’une équation du premier degré à une inconnue.

On distingue deux méthodes par le calcul et une graphique.

Principe : On exprime une des deux inconnues en fonction de l’autre à l’aide d’une des équations, et l’on substitue le résultat obtenu dans l’équation restante.

Exemple : .

Dans la première équation : y = 2x – 1.

Puis en substituant y dans la deuxième équation :

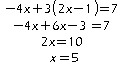
d’où, en reportant la valeur dans la première équation :

Si un couple (x;y) est solution alors x=5 et y=9

Réciproquement su x=5 et y=9, alors:

et .

Le système a pour unique solution le couple (5 ; 9).

Avantage de cette méthode :

Elle permet un calcul rapide lorsque l’on peut exprimer l’une des inconnues simplement en fonction de l’autre.

Principe : On multiplie l’une ou les deux équations par des nombres convenablement choisis de manière à ce que l’une des inconnues disparaisse par addition membre à membre.

Exemple : .

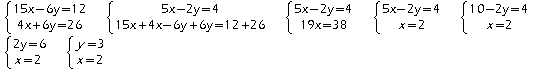
Si un couple (x;y) est solution alors x=2 et y=3

Réciproquement si x=2 et y=3, alors:

et

donc le système a pour unique solution (2;3)

Principe : On associe aux deux équations du système deux équations de deux droites. Le problème revient alors à chercher, s’il existe, le point d’intersection des deux droites. Les coordonnées de ce point constituent alors la solution du système.

Intérêt : - Cela permet de contrôler les résultats obtenus par le calcul.

- Cela permet de prédire l’existence ou non de solution, en se souvenant que :

• Deux droites parallèles ont même coefficient directeur. Dans ce cas le système correspondant n’a pas de solution.

• Deux droites confondues ont la même équation. Dans ce cas le système correspondant admet une infinité de solution.

• Deux droites sécantes ont un seul point d’intersection : le système correspondant admet alors une unique solution.

Exemple :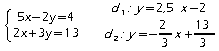

Tracé des droites associées aux fonctions affines: