Divisions. Quotients.

Propriété: On se donne a et b deux nombres entiers naturels avec b non nul. Il existe deux nombres entiers q et r tels que: et tel que: .

a est appelé le dividende de la division euclidienne de a par b et b est appelé le diviseur de la division euclidienne de a par b.

q est appelé le quotient de la division euclidienne de a par b et r le reste de la division euclidienne de a par b.

Autrement dit, en utilisant la disposition habituelle pour les calculs:

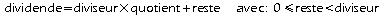
Exemple: La division euclidienne de 33 par 7 donne comme quotient 4 et reste 5.

En effet: .

Pour savoir poser une division euclidienne (vidéo d'une durée de 2'38'')

Pour cela on procède comme suit:

On peut alors conclure en disant que la division euclidienne de 370 par 17 a pour quotient 21 et reste 13.

Définition : Lorsque le reste dans la division euclidienne de a par b est nul, on dit que a est un multiple de b ou que a est divisible par b.

Exemples et contre-exemples:

35 est un multiple de 5 car:

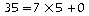
33 n'est pas un multiple de 7, car: 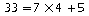, le reste de la division euclidienne de 33 par 7 est non nul.

Remarque: Les multiples d’un entier sont les produits de cet entier par 0 ; 1 ; 2 ; 3…

Exemple : Les multiples de 11 sont : 0 ; 11 ; 22 ; 33 ; 44 ; 55 ; 66 ; …

Règle : Un nombre entier est divisible par :

• 2 s’il se termine par 0 ; 2 ; 4 ; 6 ; ou 8.

• 3 si la somme de ses chiffres est un multiple de 3.

• 4 si le nombre formé par les deux derniers chiffres de ce nombre est un multiple de 4.

• 9 si la somme de ses chiffres est un multiple de 9.

• 5 si il se termine par 0 ou 5.

• 10 si il se termine par 0.

• 100 si il se termine par 00.

Définition: Le quotient de a par b (où b est un nombre non nul) est le nombre par lequel il faut multiplier b pour obtenir a.

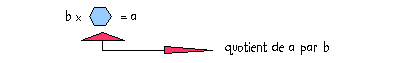
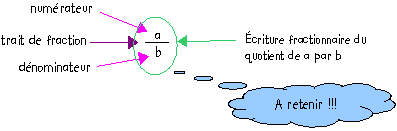
Notation: Le quotient de a par b se note . (On lit « a sur b »), ou, parfois: a:b

est appelé l'écriture fractionnaire du quotient de a par b

Exemple:

Le quotient de 21 par 3 s'écrit .

Le quotient de 19 par 28 s'écrit .

Définition: Lorsque a et b sont deux nombres entiers (avec b non nul), l'écriture s'appelle une fraction.

Exemples:

est une fraction.

n'est pas une fraction: 1,5 n'est pas un nombre entier. est simplement l'écriture fractionnaire du quotient de 1,5 par 19.

Règle: On ne change pas le quotient de a par b, lorsqu'on multiplie ou l'on divise par un même nombre non nul chacun des nombres a et b.

Autrement dit:

Exemples:

Définition: La division de a par b (où b est non nul) est l'opération qui permet de calculer la valeur décimale exacte ou approchée du quotient de a par b.

Exemples :

• où la division s'arrête:

On a donc: 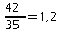ou autrement dit: .

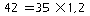• où la division ne s'arrête pas:

On a donc: . 8,33 est une valeur approchée au centième près du quotient de 50 par 6.

Règle: Pour diviser par 10, 100,1000,... un nombre décimal, on déplace la virgule de 1,2, 3, ... rang(s) vers la gauche en rajoutant éventuellement des zéros devant le nombre.

Exemple:

329 : 10 = 32,9

329 : 100 = 3,29

329 : 1000 = 0,329