Arithmétique. Ensembles de nombres.

Un nombre entier naturel est un nombre entier positif.

Rappel sur la division euclidienne:

Propriété: Soient a et b deux entiers naturels avec b non nul. Il existe un couple unique d'entiers (q,r) tels que: et tel que: . q est appelé le quotient de la division euclidienne de a par b et r le reste de la division euclidienne de a par b.

Remarques : Si le reste de la division euclidienne d'un nombre entier a par un nombre entier d est nul, alors d est appelé un diviseur de a. Il existe alors un nombre entier k tel que a=kd. On dit aussi que a est un multiple de d.

Propriété : Un nombre est divisible par:

• 2 si il se termine par 0; 2; 4; 6; 8.

• 3 si la somme de ses chiffres est un multiple de 3.

• 5 si il se termine par 0 ou 5.

• 9 si la somme de ses chiffres est un multiple de 9.

• 10; 100 … si il se termine par 0; 00 etc…

Propriété: Si deux entiers naturels admettent d comme diviseur, alors leur somme et leur produit admettent aussi d comme diviseur.

Preuve: Soient a et b les deux entiers naturels. Comme d est un diviseur de a, il existe un entier k tel que: . De même, il existe un entier k' tel que: .

Par suite: et donc d est un diviseur de a + b.

Supposons maintenant. On a: et donc d est un diviseur de a – b. Le raisonnement est identique si .

Définition: On appelle diviseur commun à deux nombres a et b tout nombre d qui est à la fois un diviseur de a et de b.

Définition: L'ensemble des diviseurs communs à deux nombres a et b admet un plus grand élément, appelé Plus Grand Commun Diviseur et noté PGCD(a; b).

Méthodes de recherche:

• Calcul d'un PGCD par soustractions successives:

Cette méthode est basée sur le fait que si d est un diviseur de deux entiers a et b (avec a<b), alors d est aussi un diviseur de a – b. On remplace la recherche du PGCD de a et b par celle du PGCD de b et a-b. Le processus s'arrête quand on obtient 0, le PGCD est alors le dernier nombre non nul.

Exemple:



 

• Calcul d'un PGCD par divisions successives: algorithme d'Euclide

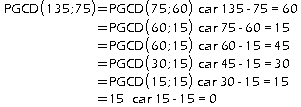
Cette méthode est basée sur le fait qu'un diviseur de deux entiers naturels a et b, est aussi un diviseur de b et du reste de la division euclidienne de a par b. On réitère jusqu'à obtenir un reste nul, le PGCD est alors le dernier reste non nul.

Exemple:



Remarque: A travers cet exemple, on perçoit l'efficacité de cet algorithme par rapport à celui des soustractions successives, puisqu'il permet d'arriver à la réponse en trois étapes au lieu de six précédemment. Aussi, on priviligiera systématiquement cet algorithme, quand on a le choix.

Définition: Deux nombres entiers non nuls sont dits premiers entre eux si leur PGCD vaut 1.

Exemples:

• 135 et 75 ne sont pas premiers entre eux car leur PGCD vaut 15.

• 45 et 28 sont premiers entre eux car leur PGCD vaut 1.

Définition: Une fraction non simplifiable est dite irréductible.

Propriété: Une fraction est irréductible lorsque son numérateur et son dénominateur sont premiers entre eux.

Méthode: Pour rendre une fraction irréductible, il suffit de diviser le numérateur et le dénominateur par leur PGCD.

Exemples:

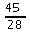• est une fraction irréductible car 45 et 28 sont premiers entre eux.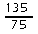

• n'est pas une fraction irréductible, car PGCD(135; 75) = 15. On peut donc simplifier la fraction comme suit:

.

On obtient alors une fraction irréductible.

Définitions:

• La liste des entiers naturels forme un ensemble noté N.

• La liste des nombres entiers positifs et négatifs forme un ensemble noté Z.

• La liste des nombres relatifs dont l'écriture à virgule comporte un nombre fini de chiffres forme un ensemble noté D.

• La liste des nombres qui peuvent s'écrire sous la forme p/q, avec p entier relatif et q entier relatif non nul, forme un ensemble noté Q.

Remarques:

• L'ensemble N est une partie de Z.

• L'ensemble Z est une partie de D.

• L'ensemble D est une partie de Q. Pour s'en convaincre, on peut toujours mettre un nombre à virgule sous la forme d'une fraction de dénominateur une puissance de 10.

Existence de nombres n'appartenant pas à Q: irrationalité de .

Pour prouver cela, il faut effectuer un raisonnement par l'absurde. Supposons que soit un rationnel, alors il existe deux entiers naturels p et q, premiers entre eux, tels que: .

On a alors: et donc: et donc est pair, par suite p est pair (en effet si p était impair, alors le serait aussi (voir plus loin)) et il existe donc k tel que: . Par suite, et donc: .

Par suite, q est pair, et il existe k' tel que: . Et donc p et q ont un diviseur commun, supérieur strictement à 1, et donc ne sont pas premiers entre eux: contradiction.

C'est donc que l'hypothèse faite au départ n'était pas la bonne: .

Définition: Il existe d'autres nombres ne pouvant pas se mettre sous la forme d'une fraction, tels que et . La liste de tous les nombres que nous utilisons au collège, fait partie d'un ensemble, appelé ensemble des réels, noté R.