Autour des théorèmes de Pythagore.

Propriété : Soient trois points A, B et M.

Propriété - Définition : Soit un point A, une droite d, et H le pied de la perpendiculaire à d passant par A.
        H est le point de la droite d le plus proche de A.
        En conséquence, AH est appelé la distance du point A à la droite d.

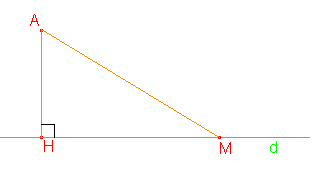
Conséquences :
        1. Quel que soit le point M de d distinct de H : AH < AM.
        2. Dans un triangle rectangle, l’hypoténuse est le côté le plus long.

Définition : La droite passant par un point du cercle et qui est perpendiculaire au rayon en ce point est appelée tangente au cercle en ce point.

Propriété : Le cercle et la tangente en un point du cercle ont un seul point commun : ce point est appelé le point de contact du cercle et de la tangente.

Théorème direct de Pythagore : Dans un triangle rectangle le carré de l’hypoténuse est égal à la somme des carrés des côtés adjacents à l’angle droit.

Exemple :

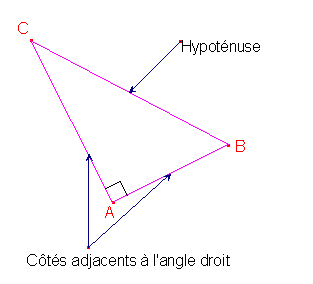
Dans le triangle ABC, rectangle en A, on a, d’après le théorème direct de Pythagore : BC² = AB² + AC².

Théorème réciproque de Pythagore : Si dans un triangle, la somme des carrés des longueurs de deux côtés est égal au carré de la longueur du troisième côté, alors ce triangle est rectangle et a pour hypoténuse ce troisième côté.

Utilité : Cela permet de montrer qu’un triangle est rectangle.