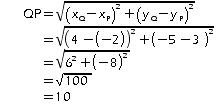Avec des coordonnées.
1. Généralités.
1.1. Repérage sur une droite.
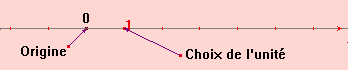
Définition :
Une droite sur laquelle on a choisi un point
origine, une unité de longueur et un sens de parcours
s’appelle une droite graduée (ou axe).
Sur un axe, le nombre associé à un point s’appelle
l’abscisse de ce point.
1.2. Repérage dans le plan.
Définition: On appelle repère du plan, la donnée de deux axes sécants en leur origine. On note un tel repère (O,I,J), où O correspond à l'origine des axes, I est le point correspondant à l'unité sur le premier axe, J est le point correspondant à l'unité sur le deuxième axe.
Définitions. Notations: On munit le plan d'un repère
(O,I,J). Chaque point M du plan est repéré par un
couple de nombres appelé coordonnées du point, la
première des coordonnées est appelée abscisse du
point, traditionnellement noté
![]() ,
la deuxième est appelée ordonnée du point,
traditionnellement noté
,
la deuxième est appelée ordonnée du point,
traditionnellement noté
![]() .
On note alors
.
On note alors
![]() .
.
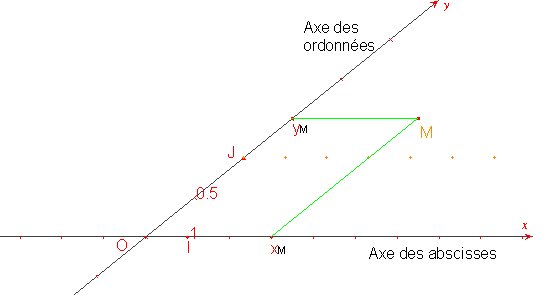
Définitions : On appelle repère orthogonal un repère dont les axes sont perpendiculaires. On appelle repère orthonormal, un repère orthogonal dont les axes sont munis de la même unité de longueur.
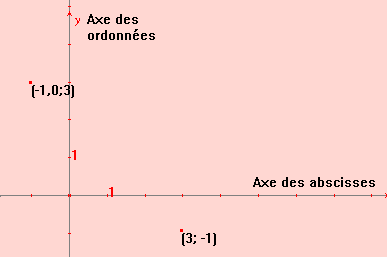
Exemple : A a
pour coordonnées (3 ; -1). 3 est l’abscisse de A et
–1 l’ordonnée de A.
2. Coordonnée d’un vecteur.
Lecture graphique des coordonnées d'un vecteur:
Définition: On
munit le plan d'un repère (O,I,J). Soit un vecteur de ce plan.
Ce vecteur est parfaitement définit par la donnée d'un
couple de nombres: le premier correspond à l'abscisse du
vecteur et le deuxième à l'ordonnée du vecteur.
Si on note
![]() ce
vecteur et
ce
vecteur et
![]() ses
coordonnées, on notera de manière synthétique:
ses
coordonnées, on notera de manière synthétique:
![]() .
.
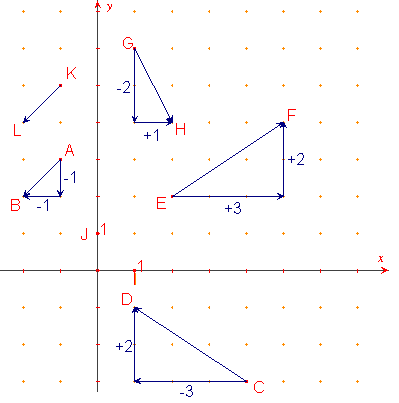
Remarque: On compte positivement lorsqu'on parcourt l'axe des abscisses (ou celui des ordonnées) dans son sens de parcours, négativement si on le parcourt en sens inverse.
Exemple:
![]() ;
;
![]() ;
;
![]() ;
;
![]() .
Le vecteur
.
Le vecteur
![]() est
un autre représentant du vecteur
est
un autre représentant du vecteur
![]() ,
ses coordonnées sont donc identiques.
,
ses coordonnées sont donc identiques.
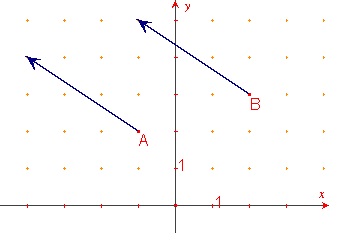
Représentation d'un vecteur dont on connaît les coordonnées:
Lorsque l'on connait les coordonnées d'un vecteur, on peut en tracer un représentant dans un repère.
Exemple:Soit![]() .
Tracer un représentant du vecteur
.
Tracer un représentant du vecteur
![]() d'origine
d'origine
![]() ,
puis d'origine
,
puis d'origine
![]() .
.
Théorème:
Soit A et B deux points de coordonnées respectives
![]() et
et
![]() ,
alors le vecteur
,
alors le vecteur![]() a
pour coordonnées
a
pour coordonnées
![]() .
.
Exemples :
M (2 ;-3) et N (3 ;-1) :
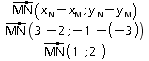
M (2 ;5) et N (1 ;0) :
3.Coordonnées du milieu d'un segment. Distance de deux points.
3.1. Coordonnées du milieu d'un segment.
Théorème: Dans le plan muni d'un repère, le milieu d'un segment a pour abscisse la demi-somme des abscisses des extrémités du segment et pour ordonnée la demi-somme des ordonnées des extrémités du segment.
Milieu d’un segment :
Soit ![]() le milieu d’un segment [AB]. Soit
le milieu d’un segment [AB]. Soit
![]() et
et
![]() les coordonnées respectives de A et B. On a :
les coordonnées respectives de A et B. On a :
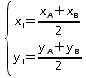
3.2. Distance de deux points.
Théorème:
On muni le plan d’un repère orthonormal. Soit A et B
deux points de coordonnées respectives
![]() et
et
![]() ,
on a :
,
on a :
![]() .
.
D’où: ![]() .
.
Exemple : P (-2 ;3) ; Q(4 ;-5)