|
Un cours de mathématiques du Collée au Lycée |
|
||
Premiers éléments de géométrie.
1. Segment, droite, demi-droite.
1.1. Le point.
"Définition ": Le point est le plus petit élément que l'on puisse trouver en géomètrie: il n'a aucun épaisseur, volume, etc... On peut dire qu'il est infiniment petit.
Notation : Un point est représenté par une croix et nommé par une lettre (généralement en majuscule).
1.2. La droite.
Définition : Une droite est définie par deux points. Elle est illimitée.
Remarque : Par deux points A et B distincts, il passe une seule droite : la droite (AB).
|
|
|
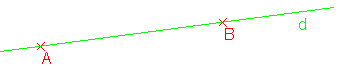
Définition : Trois points ou plus sont alignés si ils appartiennent à la même droite.
Exemple :
E, M et F sont alignés.
.
|
|
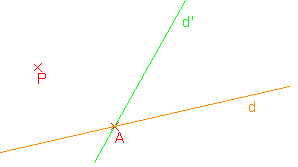
A est un point de la droite d. On écrit
P n’est
pas un point de la droite d. On écrit
Les droites d et d’ se coupent en un point A. On dit que d et d’ sont sécantes en A, ou encore que A est le point d’intersection de d et d’. |
.
.1.3. Le segment.
Définition : Un segment est limité aux deux points qui le définissent.
Exemple : Segment [AB] de longueur 5 cm.
Définition : Une demi-droite est définie par deux points : le premier qui marque son origine et le deuxième la direction où elle est illimitée.
1.4. La demi-droite.
Exemple : Demi-droite [AB) :
2. Configurations particulières de droites.
2.1. Droites parallèles.
Définition : Deux droites distinctes sont dites parallèles si elles n’ont aucun point commun.
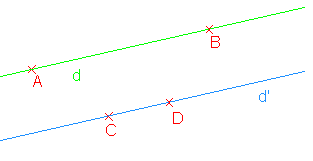
Notation : On note d//d’ ou (AB)//(CD).
2.2. Droites perpendiculaires.
Définition :
Deux droites sécantes qui se coupent en
formant un angle droit sont dites perpendiculaires.
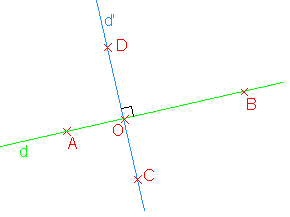
Notation : On note
ou
ou
.
2.3. Propriétés.
Propriété 1: Si deux droites sont perpendiculaires à une même troisième, alors elles sont parallèles entre elles.
Propriété 2: Si deux droites sont parallèles, alors toute perpendiculaire à l’une est perpendiculaire à l’autre.
Propriété 3:Si deux droites sont perpendiculaires, alors toute droite parallèle à l'une est perpendiculaire à l'autre.
3. Constructions.
3.1. De deux droites perpendiculaires à l’équerre.
3.2. De deux droites parallèles à l’équerre.
3.3. De deux droites parallèles au compas.
